Teoria dos Números¹

Teoria dos Números é um ramo da matemática que estuda os números inteiros. Dominar o maior número possível de tópicos da teoria dos números é importante, pois alguns problemas matemáticos se tornam fáceis (ou mais fáceis) se você conhecer a teoria por trás do problema.

Divisibilidade

Um inteiro \(n\) é divisível por um inteiro \(d\) (denotado por \(d | n\).) se houver outro inteiro \(q\) tal que \(n = d \times q\). Também é dito que \(d\) é um divisor de \(n\). Dividindo os dois lados da igualdade \(n = dq\) por \(d\) tem-se uma definição quase equivalente, ou seja, que \(\frac{n}{d}\) é um inteiro.

Exemplo

O número 12 possui 6 divisores: \(1~(1 \times 12 = 12), 2~(2 \times 6 = 12), 3~(3 \times 4 = 12), 4~(4 \times 3 = 12), 6~(6 \times 6 = 12)\) e \(12~(12 \times 1 = 12)\).

O conceito de divisibilidade traz muitas questões. A primeira é como verificar se um número é divisível por outro. Para número pequenos, que podem ser armazenados em variáveis, por exemplo, do tipo long long, pode-se usar o operador módulo ou resto da divisão (%): \(n\) é divisível por \(d\) se e somente se ǹ % d == 0. Entretanto, para números inteiros grandes a solução não é tão simples. Na Seção Aritmética Modular será discutido como implementar o operador módulo para número inteiros grandes.

Outra questão é como calcular os divisores de um número. Todo inteiro \(n\) tem pelo menos dois divisores (\(1\) e \(n\)). Para encontrar os outros divisores, pode-se usar o fato que qualquer divisor \(d\) de \(n\) deve satisfazer \(|d| \leq |n|\). Assim, pode-se testar se os inteiros entre \(1\) e \(n\) são divisores de \(n\), ou seja, um algoritmo \(O(n)\). Entretanto, sempre que tem-se um divisor \(d\), tem-se outro divisor \(q\) (veja o exemplo anterior). Por exemplo, ao afirmar que \(3\) é um divisor de \(12\), pois \(3 \times 4 = 12\), tem-se outro divisor, \(4\). Ou seja, os divisores vêm em pares. Veja outros exemplo:

Exemplo

O número 16 possui 5 divisores: \(1~(1 \times 16 = 16), 2~(2 \times 8 = 16), 4~(4 \times 4 = 16), 8~(8 \times 2 = 16)\) e \(16~(16 \times 6 = 16)\).

Dessa forma, pode-se limitar a encontrar cada elemento desses pares. Além disso, um dos valores de cada par deve ser limitado por \(\sqrt n\). Por quê? Esse limite ajuda a reduzir a complexidade do algoritmo que encontra todos os divisores de um número em \(O(\sqrt n)\). A função abaixo retorna um vector com todos os divisores de \(n\).

vector<long long> divisores(long long n) {
    vector<long long> ans;
    for(long long a = 1; a*a <= n; a++) { // (1)
        if(n % a == 0) {
            long long b = n / a;
            ans.push_back(a);
            if(a != b) ans.push_back(b);
        }
    }
    return ans; // (2)
}

x <= sqrt(n) é o mesmo que x*x <= n.
Em alguns casos, é interessante ou necessário retornar os divisores ordenados

Complemente sua leitura e seu conhecimento:

Números Primos

Um número inteiro \(n > 1\) é chamado de número primo se e somente se possui dois divisores: \(1\) e \(n\). Um número que não é primo é chamado de número composto (veja a figura abaixo). O primeiro e único número primo par é \(2\). Os próximos números primos são: \(3, 5, 7, 11, 13, \dots\). Como você deve imaginar, existe um número infinito de primos (Veja a prova aqui).

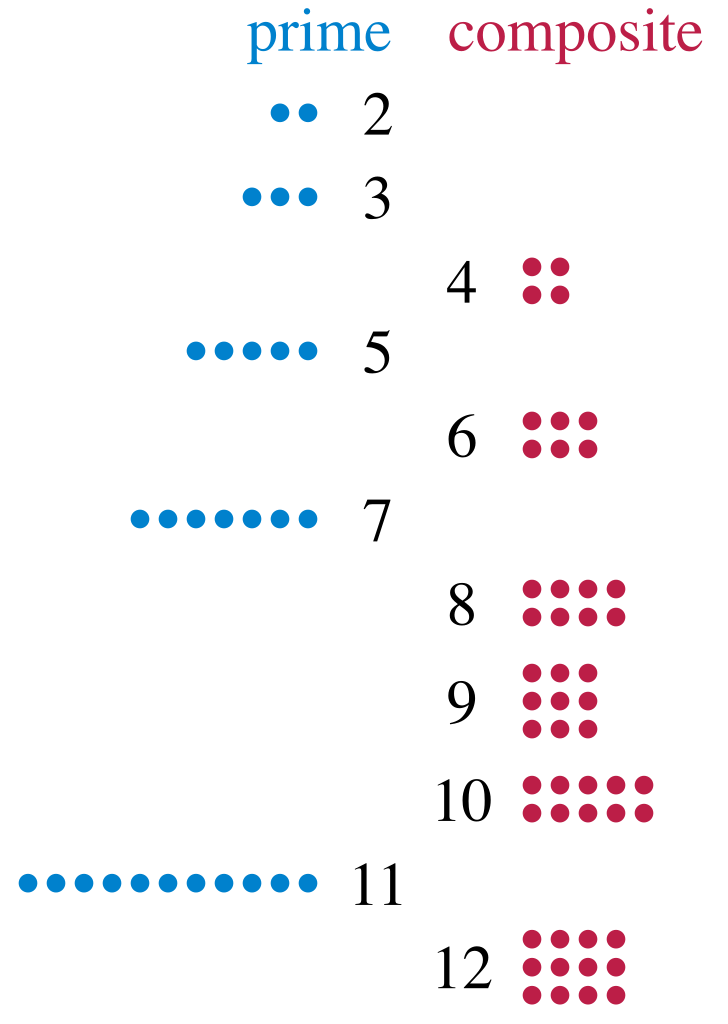
Número primo é um tópico importante da teoria dos números e a fonte de muitos problemas em programações competitivas. Por isso é de extrema importância conhecer e dominar alguns algoritmos que envolvam números primos.

Testes de Primalidade

Se um número \(n\) não é primo, então ele pode ser representado pelo produto de dois inteiros \(a \times b\), onde \(a \leq \sqrt n\) ou \(b \leq \sqrt n\). Com isso, pode-se testar se um número é primo ou não e encontrar uma decomposição (fatoração) em fatores primos em \(O(\sqrt n)\). A função abaixo verifica se um dado número \(n\) é primo ou não.

bool ehPrimo(long long n) {
    if (n < 2) 
        return false;
    for (long long x = 2; x*x <= n; x++) { // (1)
        if (n % x == 0)
            return false;
    }
    return true;
}

x <= sqrt(n) é o mesmo que x*x <= n.

Ou, alternativamente:

bool isPrimeFast(long long n) { // (1)
    if (n < 5 || n % 2 == 0 || n % 3 == 0)
        return (n == 2 || n == 3);
    long long maxP = sqrt(n) + 2;
    for (long long p = 5; p < maxP; p += 6) {
        if (p < n && n % p == 0) return false;
        if (p+2 < n && n % (p+2) == 0) return false;
    }
    return true;
}

Fonte: primes.cpp

Complemente sua leitura e seu conhecimento:

Primality tests

Decomposição em fatores primos

Todo número positivo \(n\) possui uma decomposição (fatoração) em fatores primos única: uma forma de decompor \(n\) em um produto de números primos, ou seja:

\[ n = p_1^{a_1} \times p_2^{a_2} \times \dots \times p_k^{a_k}, \]

onde \(p_i\) são números primos distintos e \(a_i\) inteiros positivos.

A função abaixo retorna um vector com a decomposição em fatores primos de \(n\).

vector<long long> factor(long long n) {
    vector<long long> ans;
    for (long long i = 2; i * i <= n; i++) {
        while (n % i == 0) {
            ans.push_back(i);
            n /= i;
        }
    }
    if (n > 1) ans.push_back(n);
    return ans;
}

Note que cada fator primo aparece no vetor o número de vezes que ele divide \(n\). Por exemplo, \(24 = 2^3 \times 3\), então o resultado da função é \([2,2,2,3]\).

Complemente sua leitura e seu conhecimento:

Crivo de Eratóstenes

O Crivo de Eratóstenes é um algoritmo para encontrar todos os números primos até um certo limite usando \(O(n \log \log n)\) operações.

A ideia do algoritmo é a seguinte: inicialmente, escreve-se todos os números entre \(2\) e \(n\). Então, marca-se todos os múltiplos de \(2\) (já que \(2\) é o menor número primo). Em seguida, pega-se o próximo valor que não foi marcado como composto, neste caso, é o \(3\). Isso significa que 3 é primo. Então, marca-se todos os múltiplos de 3 como compostos. O próximo número não marcado é o \(5\) (próximo número primo). Marca-se todos os múltiplos de \(5\). Este processo é repetido até \(n\). A animação abaixo exemplifica a execução do algoritmo para \(n = 120\).

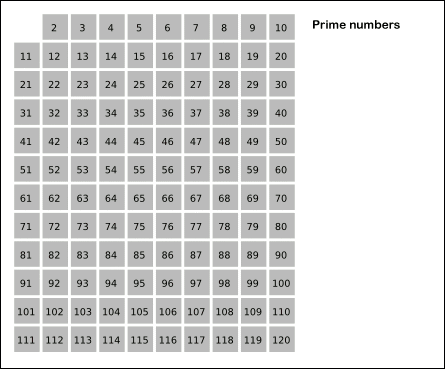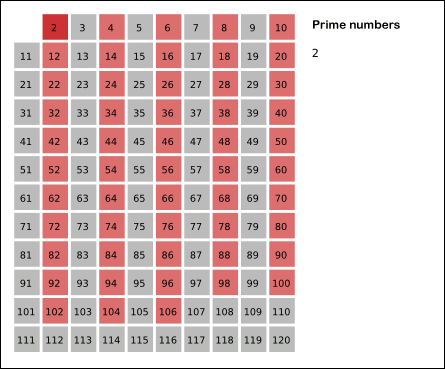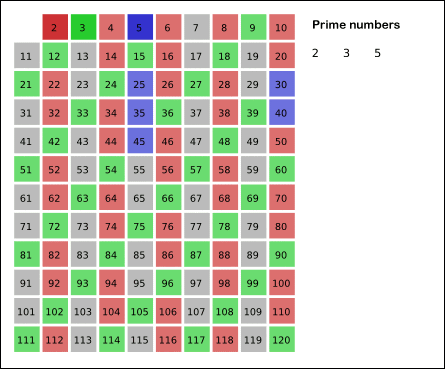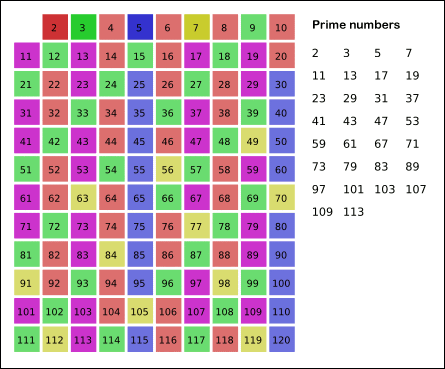
O código abaixo exemplifica uma possível implementação do algoritmo. Esse algoritmo possui complexidade \(O(n \log \log n)\) (veja a prova aqui).

vector<bool> crivo(long long n) {
    vector<bool> primo(n+1, true); // (1)
    primo[0] = primo[1] = false;
    for (long long i = 2; i <= n; i++) {
        if (primo[i] && i * i <= n) {
            for (long long j = i * i; j <= n; j += i) // (2)
                primo[j] = false;
        }
    }
    return primo;
}

Cria um array (vector) booleano de tamanho \(n + 1\), onde todas as posições são inicializadas com true.
Iteramos por todos os números divisíveis pelo primo i

Complemente sua leitura e seu conhecimento:

Primo de Mersenne

Número de Mersenne é todo número natural da forma \(M_{n}=2^{n}-1\), onde \(n\) é um número natural. Os primeiros números Mersenne são: \(0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, \dots\). Um subconjunto particularmente interessante é o constituído pelos números de Mersenne que são também primos: os primos de Mersenne. Note que nem todo número de Mersenne é primo, assim como nem todo número primo é de Mersenne.

Os primeiros primos de Mersenne são: \(M_2 = 3, M_3 = 7, M_5 = 31, M_7 = 127, M_13 = 8191, M_17 = 131071, M_19 = 524287, \dots\)

Um resultado elementar sobre os números de Mersenne afirma que se \(2^{n}-1\) é um número primo, então \(n\) também é um número primo.

Algoritmo de Euclides (MDC/MMC)

O máximo divisor comum (GCD, do inglês greatest common divisor) dos números \(a\) e \(b\), gcd(a,b), é o maior número que divide \(a\) e \(b\), e o mínimo múltiplo comum (LCM, do inglês least common multiple) de \(a\) e \(b\), lcm(a,b), é o menor número que é divisível por \(a\) e \(b\).

O algoritmo de Euclides fornece uma maneira eficiente de encontrar o máximo divisor comum de dois números. O algoritmo é baseado na seguinte definição:

\[ \gcd(a, b) = \begin{cases}a,&\text{se }b = 0 \\ \gcd(b, a \bmod b),&\text{caso contrário.}\end{cases} \]

Usando essa definição, o algoritmo é facilmente implementado usando recursão:

long long gcd(long long a, long long b) {
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

Dica

Você pode usar a função integrada __gcd(a, b) do C++.

Pode-se mostrar que o algoritmo de Euclides possui complexidade \(O(\log n)\), onde \(n = min(a,b)\).

O mínimo múltiplo comum (LCM) pode ser calculado da seguinte forma:

\[ lcm(a, b) = \frac{a \times b}{gcd(a,b)} \]

Para calcular o GCD ou LCM de mais de dois valores, pode-se calcular o valor de dois em dois (em qualquer ordem). Por exemplo:

\[ gcd(a, b, c, d) = gcd(a, gcd(b, gcd(c, d))) \]

Função totiente de Euler

A função totiente de Euler, também conhecida como função \(\phi (n)\), conta o número de inteiros entre \(1\) e \(n\), no qual são coprimos de \(n\). Dois números são coprimos se o máximo divisor comum entre eles for 1 (1 é considerado ser coprimo para qualquer número). Por exemplo, \(\phi (12) = 4\), pois 1, 5, 7 e 11 são coprimos de 12.

Abaixo estão valores de \(\phi (n)\) para os primeiros números inteiros positivos:

\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 \\ \hline \phi(n) & 1 & 1 & 2 & 2 & 4 & 2 & 6 & 4 & 6 & 4 & 10 & 4 & 12 & 6 & 8 & 8 & 16 & 6 & 18 & 8 & 12 \\ \hline \end{array}\]

A função abaixo calcula o valor de \(\phi (n)\) em \(O(\sqrt n)\).

long long phi(long long n) {
    long long result = n;
    for (long long i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            while (n % i == 0)
                n /= i;
            result -= result / i;
        }
    }
    if (n > 1)
        result -= result / n;
    return result;
}

Complemente sua leitura e seu conhecimento:

Aritmética Modular

Na aritmética modular, o conjunto de números é limitado de forma que apenas os números \(0,1,2,\dots,m−1\) são usados, onde \(m\) é uma constante. Cada número \(x\) é representado pelo número \(x \bmod m\): o resto da divisão de \(x\) por \(m\). Por exemplo, se \(m = 23\), em vez \(x = 247\), considera-se \(x \bmod 23 = 17\). Normalmente, \(m\) será um primo grande, dado no problema, normalmente, \(10^9 + 7\). A aritmética modular é usada para evitar integer overflow.

As seguintes propriedades valem no cálculo do módulo:

\[(a+b) \bmod m = (a \bmod m + b \bmod m) \bmod m\]

\[(a-b) \bmod m = (a \bmod m - b \bmod m) \bmod m\]

\[(a \cdot b) \pmod{m} = ((a \bmod m) \cdot (b \bmod m)) \bmod m\]

\[a^b \bmod {m} = (a \bmod m)^b \bmod m\]

O que significa que se a resposta está sendo computada por meio de adições, subtrações e multiplicações, e no final você precisa tirar o módulo dela, você pode tirar o módulo em todas as operações intermediárias que isso não afetará a resposta.

Exponenciação Binária

A exponenciação binária é um truque que permite calcular \(x^n\) usando apenas multiplicações \(O(\log⁡ n)\) (em vez das multiplicações \(O(n)\) exigidas pela abordagem ingênua).

Sabe-se que \(x^a \cdot x^b = x^{a+b}\). Em particular, \(x^{2b} = x^b \cdot x^b\). Logo, se o expoente \(n\) de \(x^n\) for par, pode-se dizer que \(x^n = x^{\frac{n}{2}} \cdot x^{\frac{n}{2}}\). No entanto, se \(n\) for ímpar, tem-se algo similar: \(x^n = x^{\frac{n-1}{2}} \cdot x^{\frac{n-1}{2}} \cdot x\). Dessa forma, pode-se montar a seguinte recorrência:

\[ x^n = \begin{cases} 1 &\text{se } n = 0 \\ \left(x^{\frac{n}{2}}\right)^2 &\text{se } n \text{ par}\\ \left(x^{\frac{n - 1}{2}}\right)^2 \cdot x &\text{se } n \text{ impar}\\ \end{cases} \]

Note que se \(n\) for par, o valor \(x^{n/2}\) deve ser calculado apenas uma vez. Isso garante que a complexidade do algoritmo seja \(O(\log n)\). A função abaixo calcula do valor de \(x^n\):

long long binpow(long long x, long long n) {
    if (n == 0)
        return 1;
    long long res = binpow(x, n / 2);
    if (n % 2)
        return res * res * x;
    else
        return res * res;
}

Alternativamente, sem usar recursão e usando manipulação de bits:

long long binpow(long long x, long long n) {
    long long res = 1;
    while (n > 0) {
        if (n & 1)
            res = res * x;
        x = x * x;
        n >>= 1;
    }
    return res;
}

Em alguns casos, é necessário calcular o valor de \(x^n \bmod m\). Sabendo que \((a \cdot b) \pmod{m} = ((a \bmod m) \cdot (b \bmod m)) \bmod m\), pode-se usar diretamente código anterior e apenas substituir cada multiplicação por uma multiplicação modular:

long long binpow(long long x, long long n, long long m = 1) { // (1)
    x %= m;
    long long res = 1;
    while (n > 0) {
        if (n & 1)
            res = res * x % m;
        x = x * x % m;
        n >>= 1;
    }
    return res;
}

Deixando o valor padrão de m como 1, pode-se usar essa função sem passar o valor de m como parâmetro.

Dica

Se \(m\) é um número primo, pode-se acelerar um pouco este algoritmo calculando \(x^{n \bmod(m−1)}\) em vez de \(x^n\).

Complemente sua leitura e seu conhecimento:

Binary Exponentiation

O texto dessa página são traduções e adaptações encontrados aqui: 1, 2, 3, 4 e 5 ↩

Teoria dos Números1

Divisibilidade

Números Primos

Testes de Primalidade

Decomposição em fatores primos

Crivo de Eratóstenes

Primo de Mersenne

Algoritmo de Euclides (MDC/MMC)

Função totiente de Euler

Aritmética Modular

Exponenciação Binária

Teoria dos Números¹