Algoritmos Gulosos¹

Um algoritmo é dito guloso se, em cada passo, ele faz uma escolha localmente ótima na esperança de que essa escolha leve a uma solução globalmente ótima. Um algoritmo guloso nunca retoma suas escolhas, de forma a construir diretamente a solução final. Por esta razão, algoritmos gulosos são geralmente muito eficientes. Por exemplo, uma maneira natural de se calcular o menor caminho entre os vértices \(x\) e \(y\) de um grafo pode ser sair de \(x\) e, repetidamente, seguir a aresta mais barata até se alcançar o vértice \(y\). Natural, mas errada!

A maior dificuldade em projetar um algoritmo guloso é encontrar uma estratégia gulosa que sempre produza uma solução ótima para o problema, uma vez que as escolhas localmente ótimas também devem ser globalmente ótimas. Muitas vezes é difícil provar que um algoritmo guloso funciona. Então, como saber se um algoritmo guloso resolverá determinado problema? De forma simplificada, um algoritmo guloso deve possuir dois componentes fundamentais:

Propriedade de escolha gulosa

Uma solução globalmente ótima é construída fazendo escolhas (gulosas) locais ótima. Em outras palavras, quando o algoritmo está considerando qual escolha fazer, ele escolhe a que parece melhor para o problema em questão, sem considerar resultados dos subproblemas e sem reconsiderar as escolhas anteriores.
Subestrutura ótima

A solução ótima do problema contém soluções ótimas dos subproblemas.

Como você deve ter percebido, algoritmo guloso não se refere a um único algoritmo, mas sim a uma forma de pensar que se aplica aos problemas, ou seja, não há uma (única) maneira de fazer algoritmos gulosos. Por isso, segue uma seleção de exemplos bem conhecidos para ajudá-lo a entender o paradigma guloso.

Exemplos

Seleção de tarefas

Considere o problema onde você precisa realizar algumas tarefas e você possui \(X\) (\(1 \leq X \leq 10^4\)) minutos para se realizá-las. Existem \(N\) (\(1 \leq N \leq 100\)) tarefas e cada uma requer \(a_i\) (\(1 \leq a_i \leq 100\)) minutos para serem concluídas. Qual o número máximo de tarefas que você pode/consegue finalizar?

Solução

Como você deseja concluir o número máximo de tarefas, você deve priorizar as tarefas mais rápidas, ou seja, comece realizando a tarefa que requer a menor quantidade de tempo e, em seguida, escolha outras tarefas em ordem crescente de tempo necessário. Por exemplo, considere a seguinte entrada:

\[ X = 15, N = 6, a_i = \{4, 3, 8, 4, 7, 3\} \]

Depois de ordenar o array, temos \(\{ 3, 3, 4, 4, 7, 8 \}\). Assim, dentro dos 15 minutos você pode finalizar quatro tarefas em um total de \(3+3+4+4 = 14\) minutos.

A implementação é bem simples. Ordene o array com o tempo necessário de finalização das tarefas e, em seguida, selecione o maior número possível de tarefas enquanto a soma dos tempos das tarefas for menor que \(X\).

C++Python

// Faça a leitura dos dados e armazene o tempo das tarefas em um vector 'a'
sort(all(a));
ll tempo = 0; // Quantidade de minutos usados até o momento
ll i = 0;
while (i < N && tempo + a[i] <= X) {
    // Enquanto houver tempo disponível, realize mais tarefas
    tempo += a[i];
    i++;
}
cout << i << endl;

# Faça a leitura dos dados e armazene o tempo das tarefas em uma lista 'a'
a.sort()
tempo = 0 # Quantidade de minutos usados até o momento
i = 0
while i < N and tempo + a[i] <= X:
    # Enquanto houver tempo disponível, realize mais tarefas
    tempo += a[i]
    i += 1
print(i)

Escalonamento

Muitos problemas de escalonamento podem ser resolvidos usando algoritmos gulosos. Um problema clássico é o seguinte: dados \(n\) eventos (ou tarefas) com seus horários de início e término, encontre uma programação que inclua o maior número possível de eventos. Não é possível selecionar um evento parcialmente. Por exemplo, considere os seguintes eventos:

Evento	Tempo de início	Tempo de fim
A	1	3
B	2	5
C	3	9
D	6	8

Neste caso, o número máximo de eventos é dois. Por exemplo, selecionar os eventos \(B\) e \(D\):

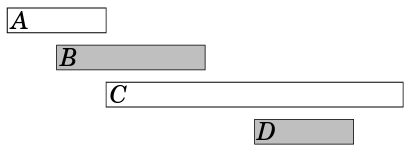
Solução — Fonte: Competitive Programmer’s Handbook

Perceba que é fácil pensar em diferentes estratégias gulosas para resolver este problema, mas qual delas funciona em todos os casos?

Algoritmo 1

A primeira ideia é ordenar os eventos de acordo com o seu "comprimento" e, enquanto for possível, ir selecionando os eventos que não se sobrepõem. Para o exemplo anterior, este algoritmo seleciona os seguintes eventos:

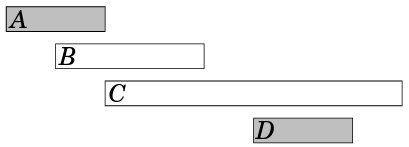
Fonte: Competitive Programmer’s Handbook

No entanto, este algoritmo falha, por exemplo, no seguinte caso:

Fonte: Competitive Programmer’s Handbook
Algoritmo 2

Outra ideia é sempre selecionar o próximo evento viável que comece o mais cedo possível. Para o exemplo, este algoritmo seleciona os seguintes eventos:

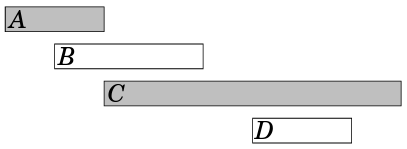
Fonte: Competitive Programmer’s Handbook

No entanto, este algoritmo também falha. Por exemplo:

Fonte: Competitive Programmer’s Handbook
Algoritmo 3

A terceira ideia é sempre selecionar o próximo evento viável que termine o mais cedo possível. Para o exemplo, este algoritmo seleciona os seguintes eventos:

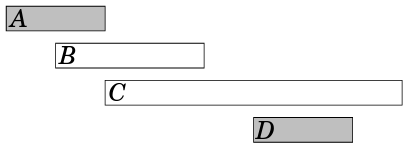
Fonte: Competitive Programmer’s Handbook

Este algoritmo sempre produz uma solução ótima. Você pode encontrar a prova neste link.

Problema da mochila fracionária

Imagine um conjunto de objetos que você gostaria de colocar em uma mochila com capacidade de \(C\) kg. Cada objeto tem um certo peso e um certo valor. Você pode escolher uma fração, entre 0% e 100%, de cada objeto para colocar na mochila. Que fração de cada objeto você deve colocar na mochila de modo a maximizar o valor total?

Atenção

No problema da mochila 0-1, não podemos fracionar os itens. Ou pegamos o item inteiro ou não o pegamos.

Solução

A ideia básica da abordagem gulosa é calcular a proporção \(valor/peso\) de cada item e ordenar os itens com base nesta proporção. Em seguida, enquanto for possível, pegue o item com a proporção mais alta que cabe totalmente na mochila. No final, adicione o próximo item o máximo que for possível. Esta estratégia gulosa produzirá uma solução ótima para o problema.

Por exemplo, considere a instância do problema da mochila fracionária que tem \(N = 5\) objetos, capacidade \(C = 50\) e os pesos e valores conforme a figura abaixo. A última linha da figura exibe a proporção do item que deve ser adicionado na mochila para que a mesma tenha valor máximo. O valor dessa solução é 1040. O valor da solução do correspondente problema da mochila 0-1 é 1000.

Fonte: Mochila fracionária

Esta estratégia gulosa funciona se for considerado o problema da mochila 0-1?

Quando o guloso falha?

Como já dito, nem sempre um algoritmo guloso irá funcionar para todo problema. Por isso, seguem dois exemplos de problemas em que ele falha.

Problema do troco

O problema do troco pode ser descrito como: dado um certo valor \(V\) e uma lista \(m\) de \(n\) moedas, supondo que exista uma quantidade ilimitada de moedas de todos os tipos, o problema consiste em descobrir qual o número mínimo de moedas para representar \(V\). Por exemplo, se \(n = 4\), \(m = \{25, 10, 5, 1\}\) centavos e se deseja representar \(V = 42\) centavos, a solução ótima é usar \(5\) moedas (\(25 + 10 + 5 + 1 + 1\)).

Existe um algoritmo guloso natural para resolver o problema: sempre selecionar a maior moeda possível para que a soma dos valores das moedas não exceda \(V\). Veja que esta estratégia gera a solução ótima do exemplo anterior. Entretanto, esta estratégia nem sempre funciona. Por exemplo, se \(n = 3\), \(m = \{4, 3, 1\}\) centavos e \(V = 6\), o algoritmo guloso irá selecionar 3 moedas \((4 + 1 + 1)\) ao invés da solução ótima que usa 2 moedas \((3 + 3)\). Para resolver este problema de forma ótima, precisamos usar Programação Dinâmica.

Problema da mochila 0-1

Diferente do problema da mochila fracionária, no problema da mochila 0-1 (ou mochila booleana), não podemos fracionar os itens, ou seja, ou pegamos o item inteiro ou não o pegamos. Neste caso, uma estratégia gulosa não funciona. Por exemplo, para a instância apresentada no problema da mochila fracionária a solução gulosa pegaria o item de peso 40 e o item de peso 10, na qual a solução é 940. No entanto, a solução ótima é selecionar os itens de peso 30 e 20, cuja solução é 1000. Para resolver este problema de forma ótima, também precisamos usar Programação Dinâmica.

Material complementar

O texto dessa página são traduções e adaptações encontrados aqui: 1, 2, 3 e 4 ↩

Algoritmos Gulosos1