Pular para conteúdo

Estrutura de Dados

Nesta parte, serão apresentados duas estruturas baseadas em árvores e uma implementação de set do GNU C++.

GNU C++ Policy-Based Sets

O compilador GNU g++ também suporta algumas estruturas de dados que não fazem parte da biblioteca padrão do C++. Essas estruturas são chamadas de estruturas de dados baseadas em políticas (Policy-Based Data Structures - PBDS). Para usar essas estruturas é necessário incluir o seguinte código:

1
2
3
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;

Alternativamente, pode-se simplificar o código anterior da seguinte forma:

1
2
#include <bits/extc++.h> 
using namespace __gnu_pbds;

Após isso, é possível definir um conjunto ordenado indexado (entre as disponíveis, essa é a principal estrutura usada em competições de programação). Esta estrutura é como o set, mas com a possibilidade de acessar os elementos de acordo com a sua posição (índice), como em um array. O código abaixo, define um conjunto ordenado indexado usando template.

1
2
template <class T> 
using indexed_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

Veja alguns exemplos de uso da definição anterior:

1
2
3
4
indexed_set<int> setInt;                // Conjunto ordenado indexado de inteiros
indexed_set<double> setDouble;          // Conjunto ordenado indexado de doubles
indexed_set<pair<int, int>> setPairInt; // Conjunto ordenado indexado de pares de inteiros
indexed_set<Pessoa> setPessoa;          // Conjunto ordenado indexado de Pessoas (precisa do operator<)

Além das operações comuns do set (insert, erase, size, clear, find, begin, end), ainda existem duas funções muito úteis e que justificam o uso do PBDS:

  • find_by_order(k): retorna um iterador para o \(k\)-ésimo menor elemento (contando a partir de zero) do conjunto em tempo \(O(\log n)\);
  • order_of_key(x): retorna ao número de itens estritamente menores que o x em tempo \(O(\log n)\).

Veja um exemplo completo de utilização do PBDS (Fonte: pbds.cpp):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
#include <bits/extc++.h> // pbds
using namespace std;
using namespace __gnu_pbds;

template <class T> 
using indexed_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

int main() {
  int n = 9;
  vector<int> A = {71, 10, 2, 4, 23, 7, 10, 15, 23, 50, 65, 71};
  indexed_set<int> iset;
  for (int i = 0; i < A.size(); ++i)             // O(n log n)
      iset.insert(A[i]);
  cout << "Set size: " << iset.size() << "\n";   // 9

  for (auto x: iset)
    cout << x << " ";
  cout << "\n";

  // O(log n) select
  cout << *iset.find_by_order(0) << "\n";        // 1-smallest = 2
  cout << *iset.find_by_order(n-1) << "\n";      // 9-smallest/largest = 71
  cout << *iset.find_by_order(4) << "\n";        // 5-smallest = 15
  // O(log n) rank
  cout << iset.order_of_key(2) << "\n";          // index 0 (rank 1)
  cout << iset.order_of_key(71) << "\n";         // index 8 (rank 9)
  cout << iset.order_of_key(15) << "\n";         // index 4 (rank 5)

  iset.erase(2);
  cout << "Set size: " << iset.size() << "\n";   // 8

  return 0;
}

Complemente sua leitura e seu conhecimento:

Fenwick (Binary Indexed) Tree

Considere o seguinte problema:

Você possui \(n\) caixas com bolinhas de gude e deseja:

  1. Adicionar bolinhas de gude a caixa \(i\);

  2. Saber a quantidade de bolinhas de gude que existem da caixa \(a\) até a caixa \(b\), ou seja, a soma das bolinhas nas caixas \([a, a+1, a+2, \dots, b]\).

O objetivo é implementar essas duas operações de forma eficiente. Esse problema é conhecido como Range Sum Queries (RSQ).

Uma abordagem ingênua, mostrada abaixo, possui \(O(1)\) para a operação 1 e \(O(n)\) para a 2. Se forem feitas \(m\) operações 2, no pior caso, a complexidade de tempo será \(O(n*m)\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
vector<ll> caixas(n, 0);

void add(vector<ll>& caixas, ll i, ll n) { // O(1)
    caixas[i] += n;
}

void sum(vector<ll>& caixas, ll a, ll b){ // O(n)
    ll s = 0;
    for(ll i = a; i <= b; i++) 
        s += caixas[i];
    return s;
}

Para responder range sum queries em sequências dinâmicas com melhor complexidade é preciso usar estruturas mais sofisticadas, que permitam a atualização das somas pré-computadas de forma eficiente. Uma destas estruturas é a Binary Indexed Tree (BIT ou Fenwick Tree), proposta por Peter M. Fenwick em 1994. Usando BIT, ambas as operações são feitas em \(O(\log n)\).

A ideia da BIT é que, assim como um número pode ser representado como uma soma de algumas potências de dois, uma soma cumulativa pode ser representada como uma soma de algumas somas cumulativas parciais. Para isso, cada índice \(i\) no array de soma cumulativa é responsável pela soma cumulativa do índice \(i\) até \((i - (1<<r) + 1)\), onde \(r\) representa a posição do último bit 1 da representação binária de \(i\) (o \(p(i) = (1<<r)\) também pode ser visto como a maior potência de \(2\) que divide \(i\)). Por exemplo, o índice \(15_{10} = 1111_2\) ficará responsável pela soma do intervalo \(15 - (1<<0) + 1 = 15 - 1 + 1\) a \(15\). Já o índice \(12_{10} = 1100_2\) ficará responsável pela soma do intervalo \(12 - (1<<3) + 1 = 12 - 8 + 1 = 9\) a \(12\), e assim por diante. A tabela abaixo mostra a responsabilidade dos índices 1 a 16.

Índice Responsável pela soma parcial do intervalo
16 [01, 16]
15 [15, 15]
14 [13, 14]
13 [13, 13]
12 [09, 12]
11 [11, 11]
10 [09, 10]
09 [09, 09]
08 [01, 08]
07 [07, 07]
06 [05, 06]
05 [05, 05]
04 [01, 04]
03 [03, 03]
02 [01, 02]
01 [01, 01]

Perceba que todo índice ímpar fica responsável por um intervalo de tamanho 1 (porquê?). Já os índices \(i\) que são potência de 2, ficam responsáveis pelo intervalo \([1, i]\).

Tipicamente, a Fenwick Tree é implementada usando um array (vector), digamos ft, de modo que:

1
ft[i] = sum(i - p(i) + 1, i);

Assim, cada posição i contém a soma dos valores de um intervalo do array original cujo comprimento é p(i) e que termina na posição i. Por exemplo, como p(6) = 2, ft[6] contém o valor de sum(5,6).

Considere o seguinte array original:

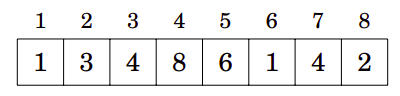
A Fenwick Tree correspondente é a seguinte:

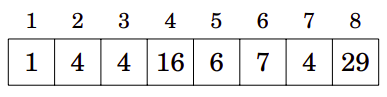
A figura abaixo mostra mais claramente como cada valor na BIT corresponde a um intervalo no array original:

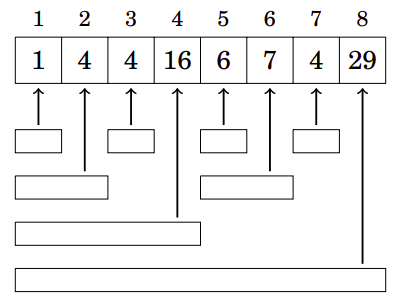
Usando uma BIT, qualquer valor de sum(1,i) pode ser calculado em tempo \(O(\log n)\), pois um intervalo \([1,i]\) sempre pode ser dividido em intervalos \(O(\log n)\) cujas somas são armazenadas na árvore. Por exemplo, o intervalo \([1,7]\) consiste nos seguintes intervalos:

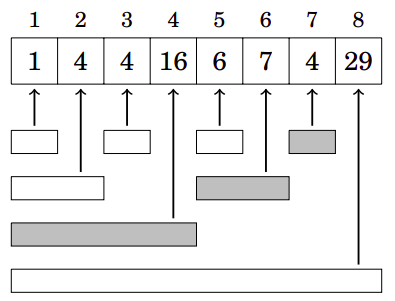
Assim, pode-se calcular a soma correspondente da seguinte forma:

\[ sum(1,7) = sum(1,4)+sum(5,6)+sum(7,7) = 16+7+4 = 27 \]

Para calcular o valor de \(sum(a,b)\) onde \(a > 1\), pode-se usar o mesmo truque que usado na soma de prefixo:

\[ sum(a,b) = sum(1,b)−sum(1,a−1). \]

Como pode-se calcular tanto \(sum(1, b)\) quanto \(sum(1, a−1)\) em tempo \(O(\log n)\), a complexidade de tempo total é \(O(\log n)\).

Além de calcular a soma parcial, também é possível/necessário atualizar o valor de uma determinada posição no array original. Após a atualização, alguns valores na BIT devem ser atualizados. Por exemplo, se o valor na posição 3 mudar, as somas dos seguintes intervalos mudam:

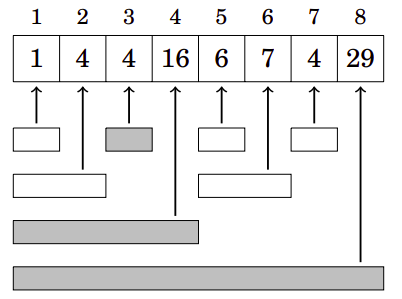
Como cada elemento do array pertence a \(O(\log n)\) intervalos na BIT, basta atualizar os \(O(\log n)\) valores na árvore.

Implementação

O primeiro passo é definir como calcular o valor de p(i), ou seja, a maior potência de \(2\) que divide \(i\). Este valor é conhecido como o bit menos significativo, abreviado lsb, da representação binária de \(i\). O função abaixo calcula esse valor:

1
2
3
4
5
6
7
int p(int i) {
    int bit = 0;
    while ((i >> bit) & 1 == 0) {
        ++bit;
    }
    return (1 << bit);
}

Essa função possui complexidade \(O(\log n)\). Entretanto, usando manipulação de bits, pode-se encontrar esse valor de forma mais eficiente. Lembre-se que um número negativo é representado usando complemento de 2, ou seja, pega-se a representação binária de x, inverte-se os bits e adiciona 1 (ignorando o resto final). Por exemplo, considere x = 108 e que os valores são representados em 8 bits:

1
2
3
 x = 01101100
~x = 10010011
-x = 10010100

Observe que os bits mais significativos que o lsb são diferentes para x e -x, enquanto o lsb e os 0s seguintes são os mesmos. Portanto, x & −x dá a resposta desejada, ou seja: x & -x = 00000100. Com essa estratégia, pode-se calcular o valor de lsb, consequentemente, o valor de p(i) em \(O(1)\):

1
2
3
long long lsb(long long i) { // (1)
    return i & -i;
}
  1. Normalmente, essa função é feita como uma macro: #define lsb(i) ((i) & -(i))

A funções a seguir calculam o valor de \(sum(1,i)\) e \(sum(a, b)\), respectivamente:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
long long sum(long long i) {
    long long s = 0;
    while (i >= 1) {
        s += ft[i];
        i -= lsb(i);
    }
    return s;
}
long long sum(long long a, long long b) {
    return sum(b) - sum(a-1);
}

A seguinte função aumenta o valor do array na posição \(i\) em \(x\) (\(x\) pode ser positivo ou negativo):

1
2
3
4
5
6
void add(int i, int x) { // Normalmente, essa função também é chamada de update
    while (i < ft.size()) {
        ft[i] += x;
        i += lsb(i);
    }
}

Para construir a BIT a partir de um array original, uma primeira estratégia é iniciar o array ft com valor 0 em todas as posições. Em seguida, para cada posição \(i\), chama-se a função add passando o valor do array original como valor a ser incrementado, o que daria resultaria em \(O(n \log n)\) operações. Veja a função abaixo:

1
2
3
4
5
void build(const vector<ll>& a) {
    ft.assign(a.size() + 1, 0);
    for (ll i = 1; i < a.size(); i++)
          add(i, a[i]);
}

Entretanto, note que após atualizar o valor de ft[i], pode-se verificar se o "pai" de \(i\) é menor que \(N\) (tamanho do array). Se for, atualiza-se o "pai" também. Dessa forma, temos uma função com complexidade \(O(n)\).

1
2
3
4
5
6
7
8
9
void build(const vector<ll>& a) {
    ll m = (ll)a.size() - 1;
    ft.assign(m + 1, 0);
    for (ll i = 1; i <= m; i++) {
          ft[i] += a[i];
          if (i + lsb(i) <= m)
              ft[i + lsb(i)] += a[i];
    }
}

Também é possível encontrar o menor índice \(i\) tal que soma acumulativa do intervalo \([1..i] \geq k\). Como as somas acumulativas dos valores estão ordenadas, pode-se usar a busca binária para encontrar tal índice. Basicamente, testa-se o índice do meio \(m = n / 2\) do intervalo inicial \([1..n]\) e verifica se sum(1, i) é menor que \(k\) ou não. Para cada valor de \(m\), tem-se \(O(\log n)\) operações, logo, essa função terá complexidade \(O(\log n \times \log n) = O(\log^2 n)\). O código abaixo ilustra tal função:

1
2
3
4
5
6
7
8
9
ll select(ll k) {
    ll ini = 1, fim = ft.size() - 1;
    for (int i = 0; i < 30; ++i) { // (1)
        ll m = (ini + fim) / 2;
        if (sum(1, m) < k) ini = m;
        else fim = m;
    }
    return fim;
}
  1. \(2^{30} > 10^9\), normalmente é suficiente.

O código abaixo mostra uma implementação completa de uma BIT. Note que foi usado uma versão baseada em orientação à objetos, mas isso não é necessário.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <bits/stdc++.h>
using namespace std;

typedef long long  ll;
typedef vector<ll> vll;

#define lsb(i) ((i) & -(i))

class  FenwickTree {
private:
    vll ft;
public:
    FenwickTree(ll m) { ft.resize(m + 1, 0); }
    FenwickTree(const vll &a) { build(a); }

    ll sum(ll i) {
        ll s = 0;
        while (i >= 1) {
            s += ft[i];
            i -= lsb(i);
        }
        return s;
    }
    ll sum(ll a, ll b) {
        return sum(b) - sum(a-1);
    }

    void add(ll i, ll x) { 
        while (i < (ll)ft.size()) {
            ft[i] += x;
            i += lsb(i);
        }
    }

    void build(const vll& a) {
        ll m = (ll)a.size() - 1;
        ft.resize(m + 1, 0);
        for (ll i = 1; i <= m; i++) {
              ft[i] += a[i];
              if (i + lsb(i) <= m)
                  ft[i + lsb(i)] += ft[i];
        }
    }

    ll select(ll k) {
        ll ini = 1, fim = (ll)ft.size() - 1;
        for (int i = 0; i < 30; ++i) {
            ll m = ini + (fim - ini) / 2;
            if (sum(1, m) < k) ini = m;
            else fim = m;
        }
        return fim;
    }
};


int main() {
    //          1  2  3  4  5  6  7  8
    vll f = {0, 1, 3, 4, 8, 6, 1, 4, 2}; // Indice 0 não é utilizado
    FenwickTree ft(f);
    cout << ft.sum(1, 8) << "\n";   // ft[8] = 29
    cout << ft.sum(1, 3) << "\n";   // ft[3] + ft[2] = 4 + 4 = 8
    cout << ft.sum(1, 7) << "\n";   // ft[7] + ft[6] + ft[4] = 16 + 7 + 4 = 27
    cout << ft.sum(2, 4) << "\n";   // sum(1, 4) - sum(1, 1) = ft[4] - ft[1] = 16 - 1 = 15
    cout << ft.sum(6, 8) << "\n";   // sum(1, 8) - sum(1, 5) = ft[8] - (ft[5] + ft[4]) = 29 - (6 + 16) = 7
    ft.add(8, 2);                   // Aumenta em duas unidades o valor da posição 8
    cout << ft.sum(1, 8) << "\n";   // ft[8] = 31
    ft.add(8, -2);                  // Reduz em duas unidades o valor da posição 8
    cout << ft.sum(1, 8) << "\n";   // ft[8] = 29
    ft.add(8, -f[8]);               // Zera o valor da posição 8
    cout << ft.sum(1, 8) << "\n";   // ft[8] = 27
    cout << ft.select(4) << "\n";   // Indice 2, sum(1, 2) == 4, que é >= 4
    cout << ft.select(5) << "\n";   // Indice 3, sum(1, 3) == 8, que é >= 8
    cout << ft.select(25) << "\n";  // Indice 7, sum(1, 7) == 27, que é >= 25

    return 0;
}

Quando usar?

Para utilizar uma árvore de Fenwick para realizar a operação \(\odot\) em um intervalo de índices \([i,j]\) da sequência \(a_k\), é necessário que esta operação tenha duas propriedades:

  1. Associatividade: para quaisquer \(x, y, z \in a_k\), deve valer que: \((x \odot y)\odot z = x \odot (y \odot z)\);

  2. Invertibilidade: para qualquer \(x \in a_k\), deve existir um valor \(y\) tal que \(x\odot y = I\), onde \(I\) é o elemento neutro/identidade da operação \(\odot\).

Como exemplos de operações que têm ambas propriedades tem-se a adição e a multiplicação de racionais, a adição de matrizes e o ou exclusivo (xor).

Material complementar

Segment Tree

Segment tree (Árvore de Segmento ou SegTree) é outra estrutura de dados para lidar com problemas de consulta em intervalos. O que torna as SegTrees poderosas é sua capacidade de fazer atualização e consulta em intervalos com complexidade \(O(\log n)\), além do tipo da consulta ser bem abrangente. Entretanto, comparada a BIT, uma SegTree requer mais memória e é um pouco mais difícil de implementar.

A ideia da SegTree é a seguinte: cria-se uma árvore de forma que cada nó representa a informação que deseja-se saber a respeito de um segmento do vetor (por exemplo, a soma). Cada nó (exceto as folhas) possui dois filhos, um filho representa a metade esquerda do intervalo e o outro, a metade direita. Esse processo repete-se (recursivamente) até que os intervalos atinjam tamanho 1. Assim, considerando o Range Sum Queries (RSQ), o nó raíz da árvore armazena a soma de todo o array, ou seja, a soma do segmento \(a[0 \dots n-1]\). Em seguida, essa segmento é dividido em dois: o filho da esquerda fica responsável pelo calcular/armazenar a soma da metade da esquerda do segmento (ou seja, \(a[0 \dots n/2]\)) e o filho da direita responsável pela metade da direita do segmento (ou seja, \(a[n/2+1 \dots n-1]\)). Cada um desses nós é novamente dividido e calcula-se a soma de cada novo intervalo. Repete-se o processo até todos os segmentos atingirem tamanho 1. Nesse link você encontra uma demonstração visual de como a SegTree funciona.

Veja uma representação visual de uma SegTree para o array a = [1,3,−2,8,−7]:

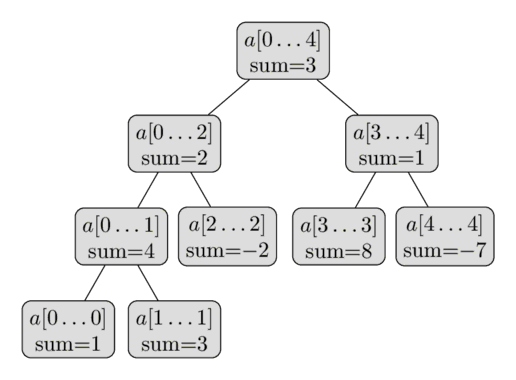
SegTree

Fonte: Algorithms for Competitive Programming

Note que o primeiro nível da árvore contém um único nó (a raiz), o segundo nível contém 2 nós, no terceiro contém 4, e assim por diante, até que o número de nós alcance \(n\). Portanto, o número de nós, no pior caso, pode ser estimado pela soma \(1+2+4+\cdots+2^{\lceil \log_2 n \rceil}=2^{ \lceil \log_2 n \rceil+1} < 4n\).

Consultas

Suponha que deseja-se fazer uma consulta (por exemplo, calcular a soma, valor mínimo/máximo, etc.) no intervalo \(l\) e \(r\), ou seja, deseja-se fazer um consulta no segmento \(a[l \dots r]\). Para isso, deve-se percorrer a árvore de segmentos e usar os valores pré-computados dos segmentos. Considere que a consulta esteja no vértice que cobre o segmento \(a[tl \dots tr]\). Existem três possibilidades:

  1. O nó está fora do intervalo de interesse, ou seja, tr < l || r < tl. Retorne um valor neutro que não afete a cunsulta (por exemplo, se a operação for a soma, retorne 0);

  2. O nó está completamente incluído no intervalos de interesse, ou seja, tl >= l && tr <= r. Retorne a informação armazenada no nó;

  3. O nó está parcialmente contido no intervalo de interesse, ou seja, (l <= tr && tr <= r) || (l <= tl && tl <= r). Então, a consulta continua nos nós filhos.

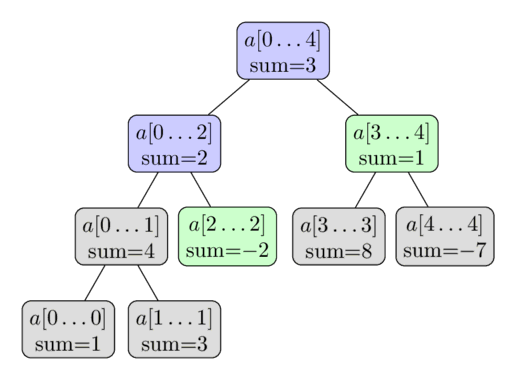
A figura abaixo ilustra esse processo para encontrar a soma do segmento \(a[2 \dots 4]\) para o array a = [1,3,−2,8,−7]. Os nós coloridos serão visitados e usa-se os valores pré-calculados dos nós verdes. Assim, o resultado será \(−2 + 1=−1\). O número de nós visitados é proporcional à altura da árvore, ou seja, \(O(\log n)\).

SegTree Query

Fonte: Algorithms for Competitive Programming

Atualizações

Fazer uma atualização no array original (por exemplo, fazer a[i] = x) implica que a SegTree também deve ter alguns nós atualizados, de modo que ela corresponda ao novo array modificado. Perceba que cada nível de uma SegTree forma uma partição do array. Portanto, um elemento a[i] apenas contribui para um segmento de cada nível. Assim, apenas \(O(\log n)\) nós necessitam ser atualizadas.

A atualização dos elementos pode ser facilmente implementada usando uma função recursiva. A função passa pelo nó atual da árvore e recursivamente chama a si mesma com um dos dois nós filhos (aquele que contém a[i] em seu segmento) e, em seguida, recalcula seu valor.

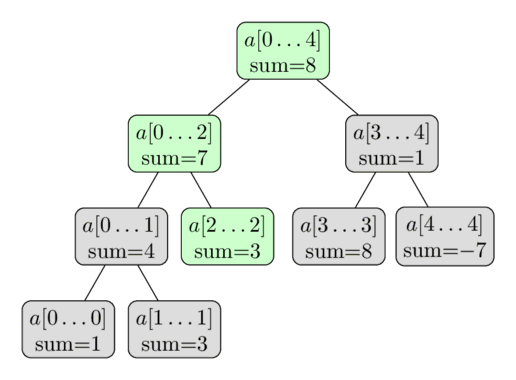
Considerando a SegTree do array a = [1,3,−2,8,−7], ao fazer a[2] = 3, os nós verdes são os nós visitados e atualizados.

SegTree Update

Fonte: Algorithms for Competitive Programming

Implementação

A primeira função a ser analisada/implementada é a build, responsável por criar a SegTree. Assim como na BIT, aqui também pode-se usar um array para armazenar os nós da SegTree (considere que o array se chama st). O índice 0 é a raíz e os filhos da esquerda e direita do índice \(i\) são os índices \(2 \times i + 1\) e \(2 \times i + 2\), respectivamente.

A raiz da SegTree representa o segmento completo [0, n-1] do array A. Para cada segmento [L, R] armazenado no índice \(i\), onde L != R, o segmento é dividido no sub-segmento [L, (L+R)/2] (armazenado no índice \(2 \times i + 1\)) e sub-segmento [(L+R)/2 + 1, R] (armazenado no índice \(2 \times i + 2\)). Essa divisão continua até que o segmento tenha tamanho 1 (isto é, L == R), o que indica que chegou-se em um nó folha e, pela definição de SegTree, esse nó deve receber o valor correspondente de A, ou seja, st[i] = A[L] ou st[i] = A[R].

A função build abaixo ilustra o processo de construção de uma SegTree a partir do array A. Perceba que foi usada a função funcao para fazer a atualização dos nós da árvore. Nesse exemplo, a SegTree será responsável por realizar a soma dos elementos (RSQ).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define filhoEsq(i) (2*(i) + 1)
#define filhoDir(i) (2*(i) + 2)

long long funcao(long long a, long long b) { // Função usada na SegTree: soma
    return a + b;
}

void build(long long i, long long L, long long R) {
    if (L > R)
        return;
    //Nó (folha) que deve conter o valor de A[L] ou A[R]
    if (L == R)
        st[i] = A[L];
    else {
        //Recursivamente constroi-se a SegTree
        long long m = L + (R - L) / 2;
        build(filhoEsq(i),     L, m);
        build(filhoDir(i), m + 1, R);
        //Após atualizar o valor dos nós filhos de 'i', atualiza-se o valor do nó 'i'
        st[i] = funcao(st[filhoEsq(i)], st[filhoDir(i)]);
    }
}

A próxima função a ser analisada/implementada é a query, responsável por fazer as consultas. Ao analisar o nó \(i\), responsável pelo intervalo [tl, tr], como explicado na seção Atualizações, existem três possibilidades. O código abaixo mostra uma implementação da função query, ela recebe como parâmetros informações sobre o nó/segmento atual (ou seja, o índice \(i\) e os limites \(tl\) e \(tr\)) e também os limites da consulta, \(l\) e \(r\). Para fazer uma consulta no intervalo [l, r], a função deve ser chamada da seguinte forma: query(0, 0, n - 1, l, r), onde n representa o número de elementos de A.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
long long query(long long i, long long tl, long long tr, long long l, long long r){
    //O nó i está fora do intervalo de interesse.
    //Retorne o elemento neutro que não afeta a consulta.
    if(tr < l || r < tl)
        return 0; // Elemento neutro da RSQ

    // O nó i está completamente incluído no intervalo de interesse. 
    // Retorne a informação contida no nó.
    if(tl >= l and tr <= r)
        return st[i];

    // Se a execução chegou nesse ponto, significa que o nó i está parcialmente 
    // contido no intervalo de interesse. Então, continua-se a procura nos nós filhos.
    long long m = tl + (tr - tl) / 2;
    return funcao(query(filhoEsq(i), tl, m, l, r), query(filhoDir(i), m + 1, tr, l, r));
}

A função update é responsável por fazer atualizações no array A e, consequentemente, na SegTree. O código abaixo mostra uma implementação da função update, ela recebe como parâmetros informações sobre o nó/segmento atual (ou seja, o índice \(no\) e os limites \(tl\) e \(tr\)), o índice \(i\) que se deseja atualizar e o novo valor a ser armazenado na posição \(i\). Para fazer A[i] = x, a função deve ser chamada da seguinte forma: update(0, 0, n - 1, i, x);, onde n representa o número de elementos de A.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
void update(long long no, long long tl, long long tr, long long i, long long novoValor){
    // Índice cujo valor deve ser atualizado
    if(tl == i and tr == i){
        st[no] = novoValor;
        A[i] = novoValor;
        return;
    }

    // O intervalo não contem o índice a ser atualizado
    if(tl > i or tr < i)
        return;

    // O intervalo contém o índice, mas deve-se chegar no nó específico. 
    // O processo é repetido recursivamente nos filhos.
    long long m = tl + (tr - tl) / 2;
    update(filhoEsq(no),    tl,  m, i, novoValor);
    update(filhoDir(no), m + 1, tr, i, novoValor);

    // Após atualizar os filhos (esquerdo ou direito), deve-se atualizar o valor do nó.
    st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
}

O código abaixo mostra uma implementação completa de uma SegTree. Note que foi usado uma versão baseada em orientação à objetos, mas isso não é necessário.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <bits/stdc++.h>
using namespace std;

typedef long long  ll;
typedef vector<ll> vll;

#define filhoEsq(i) (2*(i) + 1)
#define filhoDir(i) (2*(i) + 2)

class SegTree {
private:
    vll st, A;
    ll size;

    ll el_neutro = 0;

    ll funcao(ll a, ll b) { // Função usada na SegTree: soma
        return a + b;
    }

    ll query(ll no, ll tl, ll tr, ll l, ll r){
        //O nó está fora do intervalo de interesse. 
        //Retorne o elemento neutro que não afeta a consulta.
        if(tr < l || r < tl)
            return el_neutro;

        // O nó está completamente incluído no intervalo de interesse. 
        // Retorne a informação contida no nó.
        if(tl >= l and tr <= r)
            return st[no];

        // Se chegarmos aqui, é porque esse nó está parcialmente contido no intervalo de interesse. 
        // Então, continuamos procurando nos filhos.
        ll m = tl + (tr - tl) / 2;
        return funcao(query(filhoEsq(no), tl, m, l, r), query(filhoDir(no), m + 1, tr, l, r));
    }

    void update(ll no, ll tl, ll tr, ll i, ll novoValor){
        // Chegamos no índice que queremos atualizar o valor
        if(tl == i and tr == i){
            st[no] = novoValor;
            A[i] = novoValor;
            return;
        }

        // O intervalo que estamos não contem o índice que queremos atualizar, retorne
        if(tl > i or tr < i)
            return;

        // O intervalo contém o índice, mas temos que chegar no nó específico. 
        // Repetimos o processo recursivamente nos filhos.
        ll m = tl + (tr - tl) / 2;
        update(filhoEsq(no),    tl,  m, i, novoValor);
        update(filhoDir(no), m + 1, tr, i, novoValor);

        // Após atualizar o filho (esquerdo ou direito), precisamos atualizar o valor do nó.
        st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
    }

    void build(ll no, ll L, ll R) {
        //Chegamos no nó que deve conter o valor de A[L] ou A[R]
        if (L == R)
            st[no] = A[L];
        else {
            //Recursivamente construimos a SegTree
            ll m = L + (R - L) / 2;
            build(filhoEsq(no),     L, m);
            build(filhoDir(no), m + 1, R);
            st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
        }
    }

public:
    SegTree(ll n): st(4*n, 0), A(n, 0), size(n){}
    SegTree(const vll &a) { 
        A = a;
        st.resize(4*A.size(), 0);
        size = A.size();
        build(0, 0, size - 1); 
    }
    ll query(ll l, ll  r) {
      return query(0, 0, size - 1, l, r);
    }
    void update(ll i, ll x){
      update(0, 0, size - 1, i, x);
    } 
};

int main() {
    //       0  1  2  3  4  5  6  7  8
    vll a = {0, 1, 3, 4, 8, 6, 1, 4, 2};
    SegTree st(a);
    cout << st.query(0, 8) << "\n";   // 29
    cout << st.query(0, 0) << "\n";   // 0
    cout << st.query(0, 3) << "\n";   // 8
    cout << st.query(0, 7) << "\n";   // 27
    cout << st.query(2, 4) << "\n";   // 15
    cout << st.query(6, 8) << "\n";   // 7

    st.update(0, 10);                 // A[0] = 10

    cout << st.query(0, 8) << "\n";   // 39
    cout << st.query(0, 0) << "\n";   // 10
    cout << st.query(0, 3) << "\n";   // 18

    st.update(8, 7);                  // A[8] = 7;

    cout << st.query(8, 8) << "\n";   // 7
    cout << st.query(0, 8) << "\n";   // 44

    return 0;
}

Atualizações em Intervalos (Lazy Propagation)

Como visto, a função update atualiza apenas uma posição do array, mas em alguns casos é necessário alterar o valor de um intervalo do array, por exemplo, alterar os elementos da posição \(l\) a \(r\) para \(x\). Uma estratégia ingênua é chamar a função update para cada posição do array (complexidade \(O(n)\)). Note que se for necessário alterar todos os elementos do array, uma alternativa é alterar apenas a raiz e postergar a atualização dos outros nós. Dessa forma, os nós filhos são atualizados somente quando for realmente necessário. Esse processo é conhecido como Lazy Propagation. É importante destacar que, para implementar lazy propagation, cada tipo de SegTree vai requerer uma implementação um pouco diferente, por isso, será importante entender como essa estratégia funciona.

Na SegTree com Lazy Propagation, cada segmento (nó) terá também um valor lazy associado. Uma atualização dividirá o segmento da mesma forma feita anteriormente e definirá o valor lazy em cada segmento alcançado. Assim, sempre que um nó for analisado, seja por meio de uma atualização ou uma consulta, uma função, propagate, será chamada. Essa função fica responsável por atualizar a informação no segmento atual e passar o valor lazy para seus filhos.

Considere o problema de saber a soma dos elementos de um intervalo e que uma atualização de intervalo significa alterar o valor de todos os elementos do intervalo para um determinado valor. Para isso é necessário, além do vetor que armazena a SegTree, outros dois vetores: lazy e marked. O vetor lazy fica responsável por armazenar o valor do segmento que ainda não foi propagado para os nós filhos. Já o vetor marked (vetor booleano) indica se há uma atualização para ser feita no nó.

A função de propagação (propagate) é a função que atualiza o valor de um nó e posterga a atualização para os filhos. Essa função deve ser chamada toda vez que um nó for analisado (seja por uma atualização ou uma consulta). O código abaixo ilustra essa função.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
void propagate(ll p, ll L, ll R) { // (1)
    // Verifica se o nó precisa ser atualizado
    if (marked[p]) {
        // O valor do nó será: número de elementos que esse intervalo representa vezes o novo valor de cada elemento do intervalo
        st[p] = (R - L + 1) * lazy[p];
        // Se o nó não for uma folha, propague a atualização para os filhos.
        if (L != R) {
            lazy[filhoDir(p)] = lazy[filhoEsq(p)] = lazy[p];
            marked[filhoDir(p)] = marked[filhoEsq(p)] = true;
        }
        // Não é mais necessário atualizar esse nó
        marked[p] = false;
    }
}
  1. Parâmetros:
    • p: nó atual
    • L: limite inferior do intervalo que p representa (inclusivo)
    • R: limite superior do intervalo que p representa (inclusivo)

A função abaixo altera o valor dos elementos do intervalo [l, r] para novoValor.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void update(ll no, ll tl, ll tr, ll l, ll r, ll novoValor) { // (1)
    //Precisamos propagar a possível atualização do nó
    propagate(no, tl, tr);

    // Chegamos no índice que queremos atualizar o valor
    if (tl >= l and tr <= r) {
        lazy[no] = novoValor;
        marked[no] = true;
        propagate(no, tl, tr);
        return;
    }

    // O intervalo que estamos não contem o índice que queremos atualizar, retorne
    if (tl > r or tr < l)
        return;

    // O intervalo contém o índice, mas temos que chegar no nó específico. 
    // Repetimos o processo recursivamente nos filhos.
    ll m = tl + (tr - tl) / 2;
    update(filhoEsq(no),    tl,  m, l, r, novoValor);
    update(filhoDir(no), m + 1, tr, l, r, novoValor);

    // Após atualizar o filho (esquerdo ou direito), precisamos atualizar o valor do nó.
    st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
}
  1. Parâmetros:
    • no: nó atual
    • tl: limite inferior do intervalo que no representa (inclusivo)
    • tr: limite superior do intervalo que no representa (inclusivo)
    • l: limite inferior do intervalo que se deseja atualizar no vetor
    • r: limite superior do intervalo que se deseja atualizar no vetor
    • novoValor: novo valor dos elementos no intervalo

Versão final da classe SegTree com alguns exemplos de utilização:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include <bits/stdc++.h>
using namespace std;

typedef long long  ll;
typedef vector<ll> vll;

#define filhoEsq(i) (2*(i) + 1)
#define filhoDir(i) (2*(i) + 2)

class SegTree {
private:
    vll st, lazy;
    vector<bool> marked;
    ll size;

    ll funcao(ll a, ll b) { // Função usada na SegTree: soma
        return a + b;
    }

    void propagate(ll p, ll L, ll R) {
        if (marked[p]) {
            // O valor do nó será: número de elementos que esse intervalo representa vezes o novo valor de cada elemento do intervalo
            st[p] = lazy[p] * (R - L + 1);
            if (L != R) {
                lazy[filhoDir(p)] = lazy[filhoEsq(p)] = lazy[p];
                marked[filhoDir(p)] = marked[filhoEsq(p)] = true;
            }
            marked[p] = false;
        }
    }

    ll query(ll no, ll tl, ll tr, ll l, ll r){
        //Precisamos propagar a possível atualização do nó
        propagate(no, tl, tr);

        //O nó está fora do intervalo de interesse. Retorne o elemento neutro que não afeta a consulta.
        if(tr < l || r < tl)
            return 0;

        // O nó está completamente incluído no intervalo de interesse. Retorne a informação contida no nó.
        if(tl >= l and tr <= r)
            return st[no];

        // Se chegarmos aqui, é porque esse nó está parcialmente contido no intervalo de interesse. Então, continuamos procurando nos filhos.
        ll m = tl + (tr - tl) / 2;
        return funcao(query(filhoEsq(no), tl, m, l, r), query(filhoDir(no), m + 1, tr, l, r));
    }

    void update(ll no, ll tl, ll tr, ll l, ll r, ll novoValor){
        //Precisamos propagar a possível atualização do nó
        propagate(no, tl, tr);

        // Chegamos no índice que queremos atualizar o valor
        if (tl >= l and tr <= r) {
            lazy[no] = novoValor;
            marked[no] = true;
            propagate(no, tl, tr);
            return;
        }

        // O intervalo que estamos não contem o índice que queremos atualizar, retorne
        if (tl > r or tr < l)
            return;

        // O intervalo contém o índice, mas temos que chegar no nó específico. Repetimos o processo recursivamente nos filhos.
        ll m = tl + (tr - tl) / 2;
        update(filhoEsq(no),    tl,  m, l, r, novoValor);
        update(filhoDir(no), m + 1, tr, l, r, novoValor);

        // Após atualizar o filho (esquerdo ou direito), precisamos atualizar o valor do nó.
        st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
    }

    void build(ll no, ll L, ll R, const vll &A) {
     //Chegamos no nó que deve conter o valor de A[L] ou A[R]
     if (L == R)
      st[no] = A[L];
     else {
      //Recursivamente construimos a SegTree
      ll m = L + (R - L) / 2;
      build(filhoEsq(no),     L, m, A);
      build(filhoDir(no), m + 1, R, A);
      st[no] = funcao(st[filhoEsq(no)], st[filhoDir(no)]);
     }
    }

public:
    SegTree(ll n) : st(4 * n, 0), lazy(4 * n, 0), marked(4 * n, false), size(n) {}
    SegTree(const vll &a) {
        size = a.size();
        st.resize(4 * size, 0);
        lazy.resize(4 * size, 0);
        marked.resize(4 * size, false);
        build(0, 0, size - 1, a); 
 }
    ll query(ll l, ll  r) {
     return query(0, 0, size - 1, l, r);
    }
    void update(ll i, ll x){
     update(0, 0, size - 1, i, i, x);
    }
    void update(ll l, ll r, ll x){
     update(0, 0, size - 1, l, r, x);
    }
};

int main() {
    SegTree st(10);
    st.update(0, 4, 1);
    cout << st.query(0, 4) << "\n";   // 5
    cout << st.query(5, 9) << "\n";   // 0
    cout << st.query(0, 9) << "\n";   // 5
    cout << st.query(0, 0) << "\n";   // 1
    cout << st.query(5, 5) << "\n";   // 0

    st.update(5, 9, 2);
    cout << st.query(0, 4) << "\n"; // 5
    cout << st.query(5, 9) << "\n"; // 10
    cout << st.query(0, 9) << "\n"; // 15
    cout << st.query(0, 0) << "\n"; // 1
    cout << st.query(5, 5) << "\n"; // 2

    st.update(0, 9, 1);
    cout << st.query(0, 4) << "\n"; // 5
    cout << st.query(5, 9) << "\n"; // 5
    cout << st.query(0, 9) << "\n"; // 10
    cout << st.query(0, 0) << "\n"; // 1
    cout << st.query(5, 5) << "\n"; // 1

    st.update(5, 20);
    cout << st.query(0, 4) << "\n"; // 5
    cout << st.query(5, 9) << "\n"; // 24
    cout << st.query(0, 9) << "\n"; // 29
    cout << st.query(0, 0) << "\n"; // 1
    cout << st.query(5, 5) << "\n"; // 20

    return 0;
}

Material complementar

Disjoint Set Union (DSU)

Para entender DSU, considere o seguinte problema (extraído desse link): suponha que exista um grupo de \(N\) amigos em um jogo. Inicialmente, cada um deles joga contra todos os outros. Conforme o jogo avança, alianças são formadas entre eles. A relação de aliança é transitiva, o que significa que se \(A\) e \(B\) são aliados e \(B\) e \(C\) são aliados, então \(A\) e \(C\) também são aliados. Você sabe quando as alianças são formadas. Em certos momentos você precisa saber se dois amigos em particular estão no mesmo time ou não.

Uma estratégia natural seria construir um grafo e, a cada atualização, incluir uma nova aresta ligando dois vertices do grafo. Para cada consulta pode-se realizar um percurso no grafo (usando Busca em Largura ou Busca em Profundidade) começando no nó \(A\) e verificando se o nó \(B\) é visitado. Adicionar uma aresta é muito rápido, mas as consultas são lentas. Uma estratégia mais eficiente para resolver esse problema é usar Disjoint Set Union.

Um conjunto disjunto, também chamado union-find, é uma estrutura de dados que opera com um conjunto particionado em vários subconjuntos disjuntos. As duas principais operações dessa estrutura são:

  • find: Dado um elemento particular do conjunto, a função identifica o subconjunto do elemento. Para isso, a função retorna o representante do conjunto.
  • join: Une dois subconjuntos em um único subconjunto.

Um conjunto disjunto funciona representando cada componente conectado como uma árvore, onde a raiz de cada árvore é o representante do componente. O pai de cada nó é outro nó no mesmo componente. Considere o exemplo dos amigos jogando para ver como a estrutura funciona. Suponha que existam 6 amigos jogando. Inicialmente, não há alianças, então cada nó é a raiz de uma árvore (os amigos são numerados de 0 a 5):

012345

Fonte: Disjoint-set Data Structures

Em seguida, suponha que 1 e 3 se tornem aliados. Considere que o nó 1 seja escolhido como representante:

012345

Fonte: Disjoint-set Data Structures

Então 2 e 4 se tornam aliados:

012345

Fonte: Disjoint-set Data Structures

Os amigos 0 e 5 são os próximos. Considere que 5 seja escolhido como representante:

012345

Fonte: Disjoint-set Data Structures

Finalmente, uma aliança é formada entre 4 e 3. Nesse caso, é preciso pegar a raiz de uma árvore e anexá-la como filho da raiz da outra árvore:

012345

Fonte: Disjoint-set Data Structures

Implementação

A estrutura DSU pode ser implementada usando arrays. Na implementação a seguir, o array pai contém para cada elemento o próximo elemento do encadeamento ou o próprio elemento se ele for um representante. Inicialmente, cada elemento pertence a um conjunto distinto:

1
2
3
4
5
6
vll pai;

void init(ll N) {
    pai.resize(N + 1);
    iota(pai.begin(), pai.end(), 0); // (1)
}
  1. std:iota

A função find retorna o representante do elemento x. O representante pode ser encontrado seguindo o encadeamento que começa em x. O código abaixo ilustra essa operação, note que a complexidade da função é \(O(n)\):

1
2
3
4
5
6
ll find(ll x) { 
    if(x == pai[x]) 
        return x;
    else
        return find(pai[x]); 
}

1
2
3
void join(ll a, ll b) { 
    pai[find(a)] = find(b);
}

Otimizações do Union-Find

A primeira otimização do algoritmo, conhecida como Path Compression, está na busca do representante de um elemento, ou seja, na função find. Observe que se a função find for eficiente, a função join também se torna eficiente. Note que o que gasta tempo na função são as chamadas recursivas da função que precisam passar por todos os ancestrais de um determinado elemento. Porém, pode-se usar um princípio da Programação Dinâmica: evitar o recálculo! Uma vez que calculado o representante de um elemento x (ou seja, find(x)), pode-se salvá-lo diretamente como seu pai (pai[x]=find(x);). Assim, nas próximas vezes que for calculado o valor de find(x), a função retornará seu representante rapidamente, pois ele já estará salvo em pai[x], o que evita a necessidade de percorrer todos os ancestrais que estavam entre x e o representante. Para fazer essa otimização basta que, na hora de o valor de find(x) for retornado, o mesmo seja salvo em pai[x]. Segue a implementação da função find otimizada:

1
2
3
4
5
6
ll find(ll x) { 
    if(x == pai[x]) 
        return x;
    else
        return pai[x] = find(pai[x]); 
}

Outra otimizaçao, conhecida como Union by size, altera a forma como é feita a união dos conjuntos. Na primeira implementação da função join, o segundo conjunto sempre é anexado ao primeiro, o que pode levar a árvores degeneradas. Nessa otimização, o menor conjunto (menor número de elementos) é unido ao maior conjunto. Segue a implementação da função join otimizada:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
vll pai;
vll tamanho;

void init(ll N) {
    pai.resize(N + 1);
    tamanho.resize(N + 1, 1);
    iota(pai.begin(), pai.end(), 0); 
}

void join(ll a, ll b) { 
    a = find(a);
    b = find(b);
    if (a != b) {
        if (tamanho[a] < tamanho[b])
            swap(a, b);
        pai[b] = a;
        tamanho[a] += tamanho[b];
    }
}

Material complementar