Busca¹

Busca sequencial

A forma mais intuitiva para procurar um elemento em um array é usar um loop que percorre todos os elementos do array e parando assim que o elemento buscado é encontrado. No pior caso, é necessário percorrer todos os elementos, logo a complexidade será \(O(n)\). O código abaixo verifica se x está no array:

for (int i = 0; i < n; i++) {
    if (array[i] == x) {
        // x encontrado na posição i
    }
}

Em C++, pode-se usar a função search.

Busca binária

Se os elementos do array estiverem ordenados, pode-se usar uma estratégia diferente e mais eficiente para realizar a busca: verifique se o elemento do meio do array é o elementos buscado, se for, a busca termina. Caso não seja, verique se o elemento do meio é menor que elemento buscaso, se for, repita o processo considerando apenas a segunda metade do array. Senão, considere a primeira metade do array. Assim, a cada passo da busca, o tamanho do array é reduzido a metade, logo, a complexidade do algoritmo é \(O(\log n)\).

int buscaBinaria(vector<int> v, int x) {
    int ini = 0, fim = v.size()-1;
    while (ini <= fim) {
        int meio = ini + (fim - ini) / 2; // (1)
        if (v[meio] == x) return meio;
        else if (v[meio] < x) ini = meio + 1;
        else fim = meio - 1;
    }
    return -1; // (2)
}

Evite usar meio = (ini + fim) / 2;, já que ini + fim pode gerar integer overflow.
x não está no vetor v.

Em C++, pode-se usar a função std::binary_search. As funções abaixo também são úteis e baseadas na busca binária:

std::lower_bound: retorna um ponteiro para o primeiro elemento do array cujo valor é pelo menos x;
std::upper_bound: retorna um ponteiro para o primeiro elemento do array cujo valor é maior que x;

As funções assumem que o array está ordenado. Se o valor procurado não for encontrado, é retornado um ponteiro para o elemento após o último elemento do array. Por exemplo, o código a seguir verifica se o array contém um elemento com valor x:

vector<int> v = {1, 2, 3, 5, 8, 10, 20};
int x = 10;
auto k = lower_bound(v.begin(), v.end(), x);
if (k != v.end() && *k == x) {
    // x encontrado no indice k
    cout << "Valor encontrado na posição: " << k - v.begin() << endl; // (1)
}

Pode-se usar a função std::distance ao invés de k - v.begin(), ou seja, distance(v.begin(), k).

Complemente sua leitura e seu conhecimento:

Busca binária em funções monotônicas²

Considere uma função booleana \(f(x)\) e se deseja encontrar o valor máximo (ou mínimo) de \(x\) tal que \(f(x)\) seja true. Da mesma forma que a busca binária só funciona se o array estiver ordenado, só é possivel aplicar a busca binária em uma função monótona, ou seja, é sempre não-decrescente ou sempre não-crescente.

Seja check(x) uma função que verifica uma propriedade de x. Se para todo x, check(x) = true implica check(x+1) = true, ou para todo x, check(x) = false implica check(x+1) = false, então a função check é monótona.

Suponha a função check abaixo que verifica se um elemento é maior ou igual a x. Se x = 11 e o vetor v = [1, 2, 3, 5, 8, 11, 12, 14, 16], então teremos o seguinte vetor de saída ao aplicarmos check em v: [0, 0, 0, 0, 0, 1, 1, 1, 1, 1].

bool check(int val) {
    return val >= x;
}

Dessa forma, a função check para essa situação é monótona e isso é relevante porque se um valor do vetor satisfizer a condição, todos os valores a direita também vão satisfazê-la, e de forma análoga, todos os valores a esquerda de um índice que não satisfaz a condição, também não vão satisfazer, e é isso que nos permite aplicar busca binária. Além disso, a função check só se torna monótona nesse exemplo quando o vetor está ordenado, por isso a busca binária só é feita em vetores ordenados.

Como encontrar o menor valor que torna check verdadeiro? R. inicia-se o processo "chutanto" um intervalo onde a resposta com certeza estará. Para cada intevalo, checa-se o meio e, dependendo da resposta, descarta-se os elementos a direita ou a esquerda, mas sempre divide-se o tamanho do intervalo por 2, até que o intervalo tenha tamanho 1. Veja uma solução:

int l = a;// sei que a resposta não é menos que a
int r = b;// sei que a resposta não é mais que b

while(r > l+1){// repita enquanto o intervalo tiver tamanho > 2
    int mid = l + (r - l)/2;
    if(check(mid)){ // mid é válido
        r = mid; // como queremos minimizar a resposta, e mid é uma resposta válida
                 //descartamos tudo a direita de mid (mas não mid)
    }
    else{
        l = mid + 1; // Se mid não é válido, descartamos ele e tudo abaixo.
    }
}
// Ao final desse laço, a resposta pode estar em l ou r.
// Queremos minimizar a resposta, então se l for válido,
// ficaremos com l, e caso contrário,  com r
int ans = r;
if(check(l)) ans = l;

Exemplo: Encontrar o maior valor de \(x \in [0, 10]\) tal que \(x^2 \leq 30\).

bool check(int val) {
    return val*val <= 30;
}
int lastTrue(int ini, int fim) {
    ini--; // Se nenhum valor no intervalor for true, retorna ini - 1
    while (ini < fim) {
        int m = ini + (fim - ini) / 2;
        if (check(m)) ini = m; // (1)
        else fim = m - 1; // (2)
    }
    return ini;
}

Se check(m) é true, então todos os números menores que m também serão true.
Se check(m) é false, então todos os números maiores que m também serão false.

Two-Pointers

Na técnica chamada Two-Pointers dois "apontadores" caminham pelo vetor. Normalmente, esses apontadores são "colocados" nas extremidades opostas do vetor e caminham um em direção ao outro, como mostra a figura abaixo.

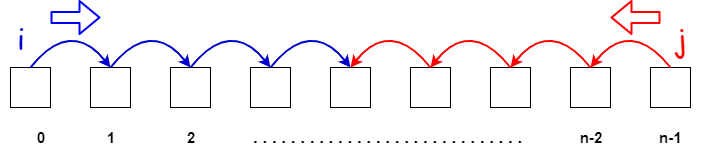
Você consegue pensar em como usar esse técnica para resolver o problema de inverter os elementos de um vetor sem usar um vetor auxiliar? A ideia é simples: coloque cada apontador (digamos i e j) em uma extremidade do vetor, ou seja, i = 0 e j = n - 1, e, a cada iteração, troque os elementos que estão nas posições i e j (ou seja, v[i] <-> v[j]). Após a troca, incremente o apontador i e decremente o apontador j. Repita esse processo enquanto i < j. A figura abaixo ilustra parte desse processo.

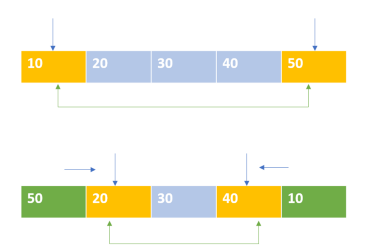
O código abaixo ilustra essa estratégia (note a simplicidade):

void inverte(vector<int> &v) { // (1)
    int i = 0;
    int j = v.size() - 1;
    while ( i < j ) {
        swap(v[i], v[j]); // (2)
        i++;
        j--;
    }
}

A std::reverse também pode ser usada com o mesmo objetivo. O intuito é mostrar com a técnica Two-Pointers funciona.
std::swap